Symmetrical Component Analysis

Decoding Unbalanced Systems • Enhancing Fault Diagnosis • Empowering Grid Stability

Introduction to Symmetrical Components

Symmetrical Component Analysis is a powerful technique used to simplify the study of unbalanced three-phase systems. It breaks down complex, asymmetrical voltages or currents into three balanced sets: positive-sequence, negative-sequence, and zero-sequence components.

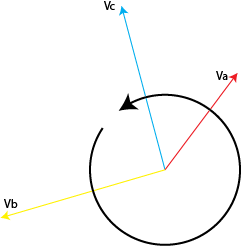
Fundamental Components Diagram
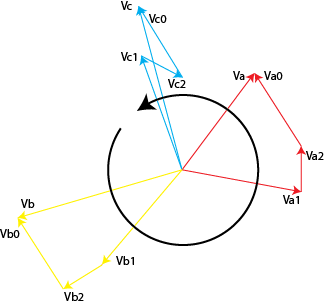
Full Symmetrical Components Diagram

Positive-Sequence Component

This component represents a balanced set of phasors rotating in the same direction as the original system. It reflects normal operating conditions and is used in load flow and stability analysis.

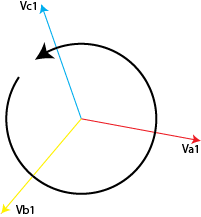
Positive Sequence Component

Negative-Sequence Component

The negative-sequence component rotates in the opposite direction and arises from faults or unbalanced loads. It can cause heating and torque pulsations in motors and generators.

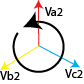
Negative Sequence Component

Zero-Sequence Component

This component consists of phasors that are equal in magnitude and phase. It typically appears in ground faults and is critical for protective relay coordination.

Zero Sequence Animation
“Symmetrical Component Analysis transforms complexity into clarity—enabling engineers to diagnose, protect, and optimize power systems.”